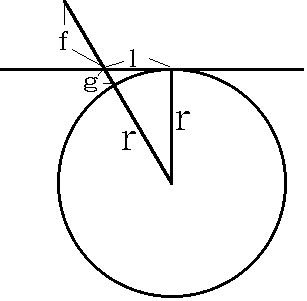
図の円は半径が r の地球を表している。
観察者から (例えば) 富士山までの距離を l とする。
富士山の眺望の下限の海抜を f+g とする。
沈み込み量はgで,富士山の眺望の下限の海抜の補正値はfである。
沈み込み量gは観察者から富士山までの距離lによって図の直角三角形から決まる長さである。 ただし空気による光の屈折も考慮して,地球の半径として r=7365
kmを用いる。
(「山岳展望の楽しみ方」（新書判、田代博著、山と渓谷社発行）を参照)
l の単位をkm,g の単位をmとすれば, 
(m)となる。
証明．図の長さの単位は km とする。三平方の定理から,
であるので,展開して整理して. g についての 2 次方程式
を得る。これを g について解き, |t| が小さい場合の近似式
を 
として用いると,
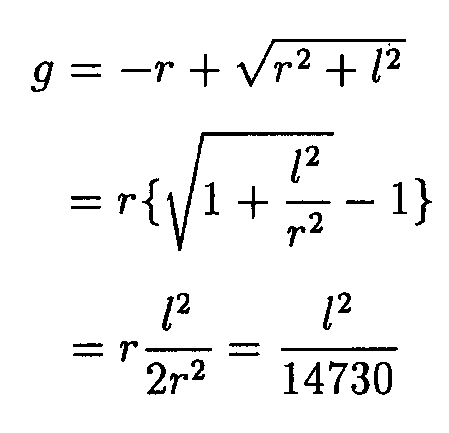
を得る(単位 km)。 kmからmに単位を変えれば, 
(m)となる。